Perhitungan Varians Excel: Panduan dengan Contoh
Varians adalah ukuran statistik yang memberi tahu kita seberapa banyak sekumpulan angka tersebar. Ini adalah konsep penting di bidang keuangan, sains, dan banyak bidang lainnya, yang membantu kita memahami variabilitas atau penyebaran dalam kumpulan data kita. Excel menyediakan cara mudah untuk menghitung varians, sehingga dapat diakses oleh pengguna pemula dan tingkat lanjut. Pada artikel ini, kita akan mempelajari cara melakukan hal ini dengan contoh yang jelas.
Apa itu varians?
Pengantar fungsi varians Excel
Bagaimana cara menghitung varians di Excel?
- VAR.S vs VAR.P – Hitung varians dari sampel atau populasi
- VAR.S vs VARA – Menghitung varians termasuk atau tidak termasuk teks dan teks logis
Varians vs Standar deviasi
Apa itu varians?
Varians adalah istilah statistik yang menggambarkan sejauh mana angka-angka dalam suatu kumpulan data berbeda dari rata-rata, atau rata-rata, angka-angka tersebut. Pada dasarnya, ini mengukur seberapa tersebar angka-angka tersebut. Poin penting dalam memahami varians adalah menyadari bahwa varians mengkuantifikasi tingkat variasi atau dispersi dalam serangkaian nilai. Varians yang tinggi menunjukkan bahwa angka-angka tersebut tersebar; varians yang rendah menunjukkan bahwa mereka berkerumun di sekitar mean.
Contoh Sederhana untuk Mengilustrasikan Varians:
Contoh: Misalkan sebuah kelas dengan lima siswa dan nilai mereka dalam ujian matematika adalah 100. Nilainya adalah 90, 92, 88, 91, dan 89.
Hitung Rata-Ratanya: Pertama, kita mencari skor rata-rata (mean). Maksudnya adalah
Hitung Varians: Lalu, kita hitung variansnya. Ini melibatkan pengurangan rata-rata dari setiap skor, mengkuadratkan hasilnya, dan kemudian membuat rata-rata selisih kuadrat tersebut.
= [0 + 4 + 4 + 1 + 1] / 5
= 10 / 5
= 2
Bagan menampilkan penyebaran skor:
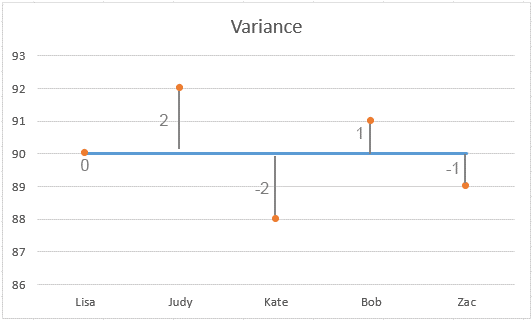
Memahami Hasilnya:
Varians Rendah: Dalam contoh ini, variansnya adalah 2. Nilai ini relatif rendah, yang menunjukkan bahwa sebagian besar skor mendekati mean (90). Semakin rendah variansnya, semakin dekat angka-angka individu dalam himpunan tersebut dengan mean.
Nol Varians: Jika semua siswa mendapat nilai tepat 90, variansnya adalah 0, yang menunjukkan tidak ada variabilitas sama sekali. Setiap skor akan sama.
Varians Tinggi: Sebaliknya, varians yang lebih tinggi akan menunjukkan bahwa skornya lebih tersebar dari rata-ratanya, sehingga menunjukkan variabilitas yang lebih besar dalam kinerja siswa.
Singkatnya, varians memberi kita nilai numerik yang membantu mengukur seberapa besar penyimpangan skor (atau serangkaian angka) dari nilai rata-rata, sehingga memberikan wawasan tentang konsistensi atau variabilitas data.
Pengantar fungsi varians Excel
Excel menyediakan beberapa fungsi untuk menghitung varians, masing-masing dirancang untuk skenario data yang berbeda.
Memahami fungsi-fungsi ini sangat penting untuk analisis statistik yang akurat
VAR (Contoh Varians, hanya menyertakan angka):
- Menghitung varians berdasarkan sampel suatu populasi.
- Paling baik digunakan saat menganalisis sebagian data untuk menyimpulkan keseluruhan.
VAR.P (Varians Populasi, hanya mencakup angka):
- Menghitung varians untuk seluruh populasi.
- Ideal ketika Anda memiliki data lengkap dan bukan hanya sampel.
TONGKAT (Contoh Varians, termasuk teks dan logika):
- Mirip dengan VAR.S tetapi menyertakan teks dan nilai logika dalam penghitungan (teks diperlakukan sebagai 0, TRUE sebagai 1, FALSE sebagai 0).
- Berguna ketika kumpulan data Anda berisi tipe campuran (angka, teks, dan nilai logika).
VARPA (Varians Populasi, termasuk teks dan logika):
- Versi varians populasi VARA.
- Menyertakan semua jenis data dalam penghitungan varians untuk seluruh populasi.
VAR (Varians Sampel Lama):
- Versi VAR.S yang lebih lama, terutama digunakan di Excel 2007 dan versi lebih lama.
- Disarankan untuk menggunakan VAR.S dalam versi yang lebih baru untuk konsistensi dan kejelasan.
VAR (Varians Populasi Lama):
- Versi lama VAR.P.
- Seperti VAR, disarankan untuk menggunakan VAR.P di versi Excel yang lebih baru.
Perbedaan dan Perbandingan:
- Sampel vs. Populasi: VAR.S dan VARA untuk sampel, sedangkan VAR.P dan VARPA untuk seluruh populasi.
- Pertimbangan Tipe Data: VARA dan VARPA menyertakan teks dan nilai logika dalam penghitungan, tidak seperti VAR.S dan VAR.P.
- Fungsi Warisan vs. Modern: VAR dan VARP adalah fungsi lama dan dapat digantikan oleh VAR.S dan VAR.P untuk kompatibilitas yang lebih baik dengan versi Excel saat ini.
Tabel perbandingan:
| fungsi | Tipe Data Dipertimbangkan | Populasi atau Sampel | Use Case |
| VAR | Hanya Angka | Contoh | Varians sampel untuk data numerik |
| VAR.P | Hanya Angka | Populasi | Varians populasi untuk angka |
| TONGKAT | Angka, Teks, Logika | Contoh | Varians sampel untuk data campuran |
| VARPA | Angka, Teks, Logika | Populasi | Varians populasi untuk data campuran |
| VAR | Hanya Angka | Contoh | Fungsi lama untuk varians sampel |
| VAR | Hanya Angka | Populasi | Fungsi warisan untuk populer |
Bagaimana cara menghitung varians di Excel?
Di bagian ini, kami akan memberikan dua contoh untuk mendemonstrasikan cara menghitung varians di Excel dan menjelaskan perbedaan antara berbagai fungsi varians. Hasilnya, Anda akan melihat bahwa fungsi varians yang berbeda menghasilkan hasil yang sangat berbeda untuk contoh data yang sama.
VAR.S vs VAR.P – Hitung varians dari sampel atau populasi
Contoh: Menghitung varians untuk sampel kecil suatu populasi vs seluruh populasi.
Contoh: Hitung varians untuk nilai di kolom A2:A12.
Rumus: Pilih sel kosong dan ketik salah satu rumus di bawah ini sesuai kebutuhan, lalu tekan Enter kunci.
-
Mendapatkan varians untuk sampel kumpulan data besar (misalkan nilai di A2:A12 adalah bagian dari kumpulan data besar)
=VAR.S(A2:A12)
-
Mendapatkan varians untuk seluruh populasi (misalkan nilai di A2:A12 adalah keseluruhan dataset)
=VAR.P(A2:A12)
Seperti yang Anda lihat, nilai yang sama tetapi menggunakan fungsi varians yang berbeda akan mendapatkan hasil yang berbeda.
Mengapa hasil VAR.S dan VAR.P berbeda?
- VAR: Fungsi ini digunakan ketika kumpulan data Anda mewakili sampel dari populasi yang lebih besar. Ini menghitung varians berdasarkan metode "n-1", di mana "n" adalah jumlah titik data dalam sampel. Menggunakan "n-1" dan bukan "n" sebagai penyebut akan mengoreksi bias dalam sampel, menjadikannya penduga varians populasi yang tidak bias. Ini memberikan perkiraan bagaimana data dalam sampel bervariasi di sekitar mean sampel.
- VAR.P: Fungsi ini digunakan ketika kumpulan data Anda mewakili seluruh populasi, bukan hanya sampel dari populasi tersebut. Ini menghitung varians berdasarkan metode “n”, di mana “n” adalah jumlah titik data dalam populasi. Diasumsikan bahwa kumpulan data mencakup seluruh populasi, sehingga tidak perlu melakukan koreksi bias seperti pada VAR.S.
- Singkatnya, perbedaan utamanya terletak pada penyebut rumusnya. VAR.S menggunakan "n-1" untuk memperhitungkan sifat sampel data, sedangkan VAR.P menggunakan "n" untuk data populasi yang tidak melibatkan pengambilan sampel. Bergantung pada kumpulan data Anda dan apakah itu sampel atau populasi penuh, Anda harus memilih fungsi yang sesuai untuk menghitung varians.
VAR.S vs VAR.P – Hitung varians dari sampel atau populasi
Contoh: Memutuskan apakah akan memasukkan nilai logika dan teks dalam penghitungan varians.
Contoh: Hitung varians untuk nilai di kolom A2:A12.
Rumus: Pilih sel kosong dan ketik salah satu rumus di bawah ini sesuai kebutuhan, lalu tekan Enter kunci.
-
Mendapatkan varians untuk sampel kumpulan data besar yang mengabaikan teks dan nilai logika.
=VAR.S(A2:A12)
-
Mendapatkan varians untuk sampel kumpulan data besar termasuk teks dan nilai logika.
=VARA(A2:A12)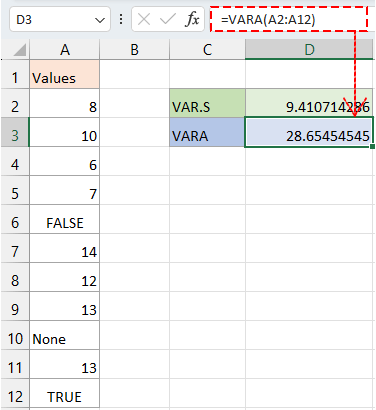
Buat Perhitungan Tanggal dan Waktu Terbang
Kutools untuk Excel's Pembantu Tanggal Waktu adalah alat yang sangat efisien yang dirancang untuk menyederhanakan penghitungan tanggal dan waktu yang rumit. Cobalah dan lihat bagaimana ini mengubah pengalaman pengelolaan data Anda!
Varians vs Standar deviasi
Kesamaan:
-
Ukuran Penyebaran:
Varians dan deviasi standar adalah ukuran statistik yang digunakan untuk menggambarkan penyebaran atau penyebaran dalam kumpulan data. Mereka mengukur seberapa jauh angka-angka individu dalam himpunan menyimpang dari mean (rata-rata).
-
Analisis Data:
Keduanya biasa digunakan dalam analisis statistik untuk memahami variabilitas data. Mereka penting dalam bidang-bidang seperti keuangan, penelitian, pengendalian kualitas, dan banyak lagi.
-
Dihitung dari Mean:
Penghitungan varians dan deviasi standar dimulai dengan mean kumpulan data. Mereka menilai variabilitas dalam kaitannya dengan nilai sentral ini.
Perbedaan:
-
Satuan Ukuran:
-
Varians: Satuan kuadrat dari data asli. Misalnya, jika data dalam satuan meter, variansinya akan dalam satuan meter persegi.
-
Deviasi Standar: Satuan yang sama dengan data asli. Melanjutkan contoh, jika data dalam satuan meter, maka standar deviasinya juga dalam satuan meter.
-
-
Interpretasi:
-
Varians: Memberikan perkiraan kuadrat yang mungkin kurang intuitif untuk diinterpretasikan karena skalanya tidak sama dengan data asli.
-
Deviasi Standar: Lebih mudah diinterpretasikan karena berada dalam satuan yang sama dengan data. Ini menunjukkan jarak rata-rata titik data dari mean.
-
-
Definisi Matematika:
-
Varians: Rata-rata selisih kuadrat dari Mean.
-
Deviasi Standar: Akar kuadrat dari varians.
-
-
Sensitivitas terhadap Nilai-Nilai Ekstrim:
-
Varians: Lebih sensitif terhadap outlier karena mengkuadratkan perbedaannya.
-
Deviasi Standar: Meskipun dipengaruhi oleh outlier, namun kurang sensitif dibandingkan varians karena akar kuadrat.
-
-
Aplikasi:
-
Perbedaan:
Digunakan ketika fokus berada pada besaran dispersi kuadrat.
Bermanfaat dalam model statistik dan komputasi yang memerlukan pengkuadratan untuk meniadakan nilai negatif.
Sering digunakan dalam model keuangan untuk penilaian risiko, karena mengukur volatilitas.
-
Standar Deviasi:
Lebih umum digunakan dalam laporan dan aplikasi sehari-hari karena kaitannya langsung dengan skala data.
Penting dalam penelitian empiris untuk memahami variabilitas.
Sering digunakan dalam kendali mutu, laporan cuaca, dan skor standar dalam ujian.
-
Kesimpulan:
Meskipun varians dan deviasi standar berfungsi untuk mengukur penyebaran kumpulan data, penerapannya berbeda karena unit pengukuran dan kemampuan interpretasinya. Deviasi standar, yang berkaitan langsung dengan skala data, cenderung lebih mudah digunakan, terutama dalam konteks praktis sehari-hari. Varians, sebaliknya, seringkali lebih cocok untuk model matematika dan statistik.
Ikhtisar dan perbandingan ini harus memberikan pemahaman yang jelas tentang kapan dan mengapa menggunakan setiap fungsi varians di Excel, sehingga memungkinkan analisis data yang lebih akurat dan bermakna. Untuk strategi Excel yang lebih mengubah permainan yang dapat meningkatkan manajemen data Anda, jelajahi lebih jauh di sini..
Alat Produktivitas Kantor Terbaik
Kutools for Excel - Membantu Anda Menonjol Dari Kerumunan
Kutools for Excel Membanggakan Lebih dari 300 Fitur, Memastikan Apa yang Anda Butuhkan Hanya Dengan Sekali Klik...

Tab Office - Aktifkan Pembacaan dan Pengeditan dengan Tab di Microsoft Office (termasuk Excel)
- Satu detik untuk beralih di antara lusinan dokumen terbuka!
- Kurangi ratusan klik mouse untuk Anda setiap hari, ucapkan selamat tinggal pada tangan mouse.
- Meningkatkan produktivitas Anda sebesar 50% saat melihat dan mengedit banyak dokumen.
- Menghadirkan Tab Efisien ke Office (termasuk Excel), Sama Seperti Chrome, Edge, dan Firefox.

Daftar Isi
- Apa itu varians?
- Pengantar fungsi varians Excel
- Bagaimana cara menghitung varians di Excel?
- VAR.S vs VAR.P – Hitung varians dari sampel atau populasi
- VAR.S vs VARA – Menghitung varians termasuk atau tidak termasuk teks dan teks logis
- Varians vs Standar deviasi
- Artikel terkait
- Alat Produktivitas Kantor Terbaik
- komentar